When you think of multiplying matrices, you probably imagine a lot of numbers flying around and crunching in the background. But what if I told you there’s a super-efficient way to make this number-crunching smoother and faster?

What is DPAS, and why should you care?

DPAS stands for Dot Product Accumulate Systolic. While it sounds technical, here’s the simple version: It’s a super-efficient operation that can perform multiplication and addition in one go, designed specifically for Intel’s Xe Core XMX Engine. This engine is optimized to handle complex AI, graphics, and machine learning tasks—anywhere massive numbers and vectors need to be processed. DPAS is like the Formula 1 car of matrix operations, blazing through calculations at breakneck speed.

Matrix Multiplication: The Monster We Need to Tame

Matrix multiplication is common in AI, simulations, and even 3D graphics. Imagine working with a 100x100 matrix—that’s 10,000 numbers on each side! Multiply those two matrices, and you’ve got a ton of operations happening. DPAS helps tackle this by making matrix multiplication super fast through smart tiling and parallel computation.

DPAS in Action: Let’s Multiply a 4x4 Matrix Using vec4

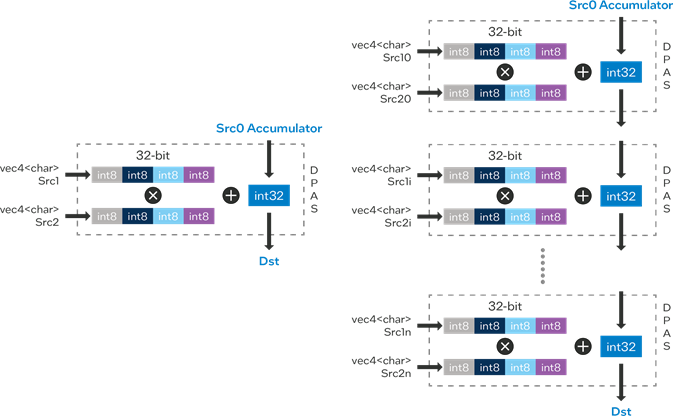
Before we get to the massive 100x100 matrix example, let’s start small. A vec4 (vector of 4 numbers) is commonly used in graphics and computations. Let’s say we want to multiply two 4x4 matrices (which consist of vec4 elements).

For simplicity, imagine you have two 4x4 matrices:

1
2
3
4
5
6
7
8
9
A = [[a11, a12, a13, a14],
     [a21, a22, a23, a24],
     [a31, a32, a33, a34],
     [a41, a42, a43, a44]]
     
B = [[b11, b12, b13, b14],
     [b21, b22, b23, b24],
     [b31, b32, b33, b34],
     [b41, b42, b43, b44]]

With DPAS, we treat this operation like a bunch of vector multiplications. Each vec4 from the first matrix is multiplied by the corresponding vec4 from the second matrix, and the results are added up in an accumulator.

For example, the dot product for the first row of matrix A with the first column of matrix B looks like this:

1
result[1,1] = (a11 * b11) + (a12 * b21) + (a13 * b31) + (a14 * b41)

And DPAS performs this in a single, efficient pass!

Scaling Up to 100x100 Matrix with 10x10 Tiling

Now, let’s get back to our big 100x100 matrix example. The problem with multiplying such large matrices is that it’s time-consuming. Instead of handling all the numbers at once, we break down the big matrix into smaller chunks, or tiles, of size 10x10.

This is where the tiled matrix multiplication concept comes into play:

1. Tiling: We divide the large matrix into smaller, more manageable 10x10 tiles.
2. DPAS Magic: Each DPAS operation processes one 10x10 tile at a time, multiplying two 10x10 matrices and adding up the results into an accumulator.
3. Reassemble: Once all the tiles are multiplied and processed, we piece them back together into the final 100x100 matrix.

Tiling with DPAS: A Fast and Efficient Approach

Instead of multiplying two giant matrices directly, DPAS lets us divide the work into tiles. Here’s how it works in our 100x100 matrix multiplication example:

1. Divide: Break the 100x100 matrix into smaller 10x10 tiles. This gives us ten 10x10 tiles on each side.
2. Multiply: DPAS takes each 10x10 tile and multiplies it with its corresponding tile from the other matrix.
3. Accumulate: As DPAS performs the multiplication, it adds the result to an accumulator. Think of the accumulator as a running total.
4. Stitch together: After all the tiles are processed, the final matrix is assembled from the results of each tile operation.

Breaking Down Tiled Matrix Multiplication

Let’s break this down in simple terms. When you multiply a matrix, each element from a row of the first matrix must be multiplied by each element in the corresponding column of the second matrix. Instead of doing all of these calculations at once, DPAS and tiling allow us to divide and conquer the problem.

For our 100x100 matrix:

• Each 10x10 tile contains 100 numbers.
• DPAS takes two 10x10 tiles (one from each matrix), multiplies them, and adds the result to the accumulator.
• Once all tiles are processed, the final result is pieced together like a puzzle.

Why DPAS + Tiling = Speed

Normally, matrix multiplication involves multiplying rows and columns one by one. But with DPAS, we’re able to parallelize these operations. By working with smaller vec4 elements and tiling the matrices into smaller chunks, DPAS pipelines the operations for faster processing.

The benefits? Massive speedup and efficient use of the hardware!

Let’s Add in a vec4 Example for Fun

Let’s revisit the vec4 example to highlight how DPAS handles vectors in matrix multiplication. When you multiply two vec4 vectors, DPAS computes the dot product:

1
vec4_dot = (a1 * b1) + (a2 * b2) + (a3 * b3) + (a4 * b4)

DPAS doesn’t just stop at one operation, though. It performs these dot products for multiple rows and columns simultaneously, thanks to the tiled approach. For a 4x4 matrix, DPAS multiplies four vec4s in one pass and accumulates the results.

Wrapping it All Up

In short, DPAS is a powerhouse that allows Intel’s Xe Core XMX Engine to crush matrix multiplication tasks by breaking down the big operations into smaller, bite-sized chunks. By tiling matrices (think dividing and conquering) and using the vec4 approach, DPAS delivers high-speed computation in the most efficient way.

So, the next time you’re working on heavy-duty AI, machine learning, or matrix math, remember: DPAS and tiling are here to save the day, making sure you get blazing-fast results without breaking a sweat!

There you have it! DPAS makes matrix multiplication faster and easier, whether you’re dealing with huge 100x100 matrices or more manageable vec4 operations.